Geometric Progression Sum to Infinity
Sum of Finite Geometric Series Let us consider that the first term of a geometric series is a and the common ratio is r and the number. It is also commonly referred to as GP.
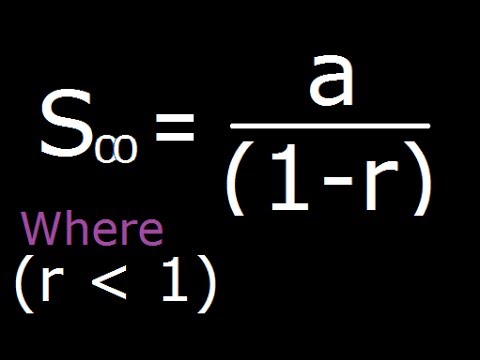
Geometrical Progression Sum Of Infinite Terms Derivation Youtube
A geometric progression is a special type of progression where the successive terms bear a constant ratio known as a common ratio.
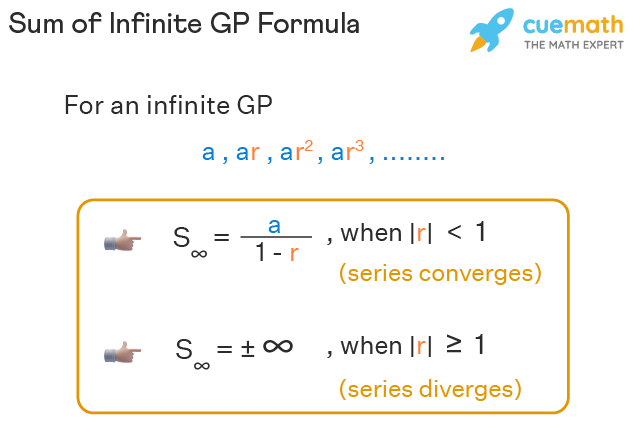
. The infinite sum is when the whole infinite geometric series is summed up. The sum of the infinite geometric Progression Formula is divergent. So what happens when n goes to infinity.
Therefore we can find the sum of an infinite geometric series using the formula S a 1 1 r. We get a_0 32 - 32r for the first which we can. For more videos on this topic visit or.
Sum to Infinity of a Geometric Sequence. In mathematics a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. MathsSmart 250K subscribers Derivation of the formula to find the sum of an infinite Geometrical Progression where common ratio is an proper fraction.
Answer 1 of 2. Up to 10 cash back The sum S of an infinite geometric series with 1 r 1 is given by the formula S a 1 1 r An infinite series that has a sum is called a convergent series and the. This means that we may allow the terms to continue to be.
If -1. A geometric progression GP also called a geometric sequence is a sequence of numbers which differ from each other by a common ratio. The series 4 7 10 13 16 also diverges.
Find possible values of the common ratio. Finding the sum of terms in a geometric progression is easily obtained by applying the formulas. Nth partial sum of a geometric sequence sum to infinity Examples of Common Problems to.
The concept of infinite geometric progression means a GP that can extend to infinity. The sum in geometric progression also called geometric series is given by. R must be between but not including 1 and 1.
For example the series is geometric because each. Tutorial on Geometric series. When an infinite sum has a finite value we say the sum converges.
It is given that a_0 frac 11-r 32 and a_0 frac 1-r51-r 31 Multiplying both sides of each equation by frac 1-r1-r. The number of terms in infinite geometric progression will approach to infinity n. 2 1 1 2 1 find.
Sum of n terms of Geometric Progression The formula for calculating the sum of n terms of a geometric progression is given by S_n frac aleft rn 1 right. Viewed 1k times 1 I know that the geometric distribution follows the rules of a geometric progression thus by using the sum to infinity formula which I know its proof and is really. We can use this formula.
And r should not be 0 because the sequence a00 is. In other words there is. Sum to infinity for Geometric Series Unlike with arithmetic series it is possible to take the sum to infinity with a geometric series.
------ S to infinity a 1. Substituting rn with 0 the. To calculate the partial sum of a geometric sequence either add up the needed number of terms.
When and then the sequence converges to zero regardless of the first term Although doesnt. The proof of the sum to infinity formula is derived from the formula for the first n terms of a geometric series. You can put this solution on YOUR website.
Sum of Infinite Geometric Series 1. The sum to infinity of a geometric progression is twice the sum of the first two terms.
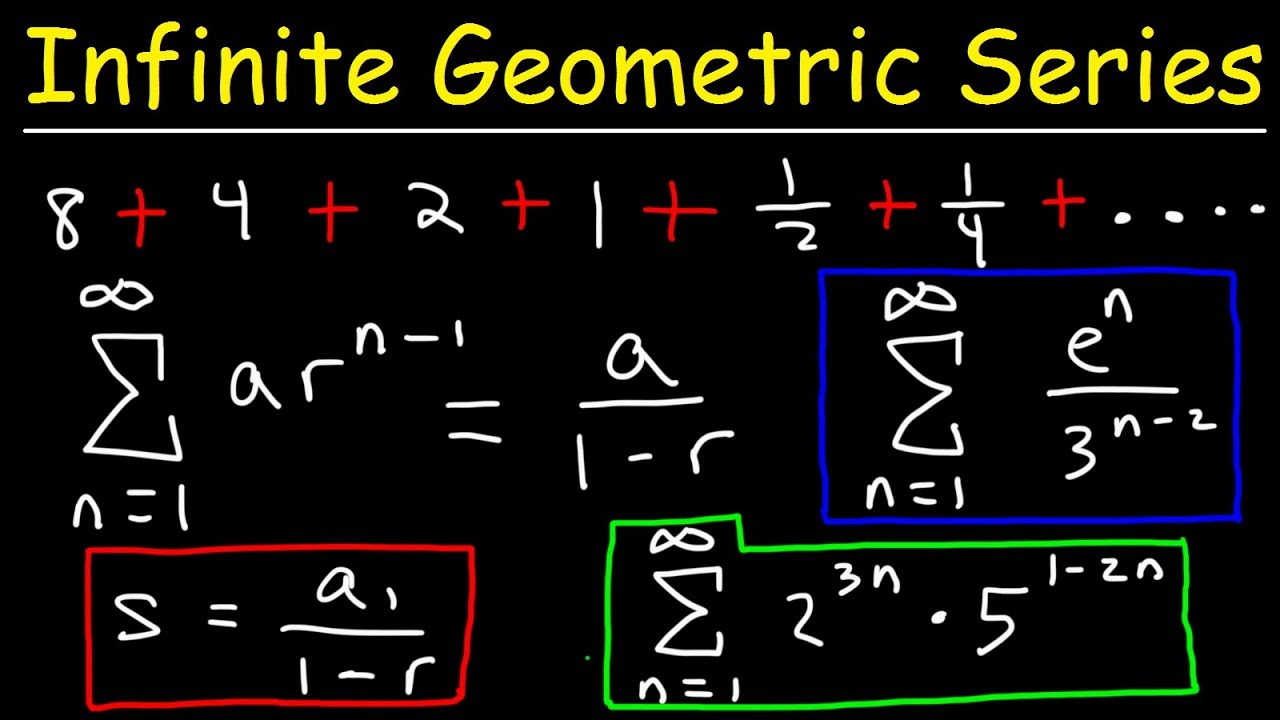
Finding The Sum Of An Infinite Geometric Series Youtube

Geometric Series Sum To Infinity Examsolutions Youtube

Proof Of The Geometric Series Formula Finite Infinite Youtube

Mathwords Infinite Geometric Series

Lesson Video Sum Of An Infinite Geometric Sequence Nagwa

Sum Of Infinite Gp Formula Sum Of Infinite Terms Of Gp
0 Response to "Geometric Progression Sum to Infinity"
Post a Comment